LK 3.2 Ciri-Ciri Fungsi

 

LK-13

Mapel                : Matematika
Materi               : Fungsi
Kelas                 : VIII (DEFGHI)
Hari/Tanggal  : Kamis, 17 September 2020    

Assalamualikum wr wb...

Selamat pagi semuanya, sekarang bertemu lagi dengan pelajaran matematika, sebelum kita mulai, marilah kita bersama-sama berdoa agar diberikan kelancaran dan kemudahan untuk memahami materi yang akan kita pelajari ini.

Pada materi sebelumnya kita sudah belajar tentang relasi, nah pada pertemuan hari ini kita akan belajar tentang fungsi. Sekarang kalian baca materi di bawah ini dengan seksama sampai kalian dapat memahaminya.

2. Fungsi atau Pemetaan

Selain fungsi dikenal juga istilah pemetaan. Keduanya memiliki makna yang sama. Pada relasi, tidak ada aturan khusus untuk memasangkan setiap anggota himpunan daerah asal ke daerah kawan. Aturan hanya terikat atas pernyataan relasi tersebut. Setiap anggota himpunan daerah asal boleh mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki pasangan. Sedangkan pada fungsi, setiap anggota himpunan daerah asal dipasangkan dengan aturan khusus. Aturan tersebut mengharuskan setiap anggota himpunan daerah asal mempunyai pasangan dan hanya tepat satu dipasangkan dengan daerah kawannya.

Perhatikan gambar di bawah ini!

Pada Gambar diatas menunjukan diagram panah untuk relasi "golongan darah" dari himpunan anak P={Ali, Budi, Dino, Yoga) ke himpunan golongan darah Q={A, B, O, AB}. Pada relasi dari himpunan P ke himpunan Q diatas diperoleh bahwa setiap anak pada himpunan P mempunyai golongan darah yang ada pada himpunan Q. Dari uraian tersebut, dapat disimpulkan bahwa setiap anggota P diapasangkan dengan tepat satu anggota Q. relasi seperti itu merupakan relasi khusus yang disebut fungsi atau pemetaan.

Jadi, Fungsi atau Pemetaan dari himpunan A ke himpunan B adalah relasi khusus yang memasangkan setiap anggota A dengan tepat satu pada anggota B

Contoh :

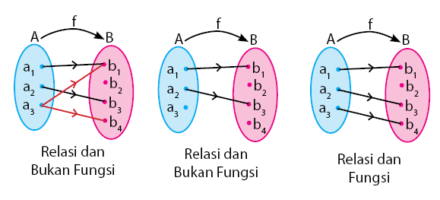
Nyatakan diagram-diagram berikut, apakah merupakan fungsi atau bukan?

Jawab:

• Gambar (1) merupakan fungsi karena setiap anggota P memiliki pasangan Q.
• Gambar (2) merupakan fungsi karena setiap anggota P memiliki pasangan Q.
• Gambar (3) bukan fungsi karena ada anggota P yaitu D yang memiliki pasangan lebih dari satu di Q yaitu 4 dan 5.
• Gambar (4) merupakan fungsi karena setiap anggota P memiliki pasangan Q.
• Gambar (5) bukan fungsi karena ada anggota P yaitu A, B, D dan E yang tidak memiliki pasangan di Q
• Gambar (6) merupakan fungsi karena setiap anggota P memiliki pasangan Q

Dari contoh-contoh diatas, dapat disimpulkan bahwa untuk mengetahui apakah relasi dari A ke B merupakan fungsi (pemetaan) atau bukan yang terutama perlu diperhatikan adalah anggota-anggota pada himpunan A. perlu diketahui bahawa, setiap relasi belum tentu fungsi, namun setiap fungsi pasti merupakan relasi.

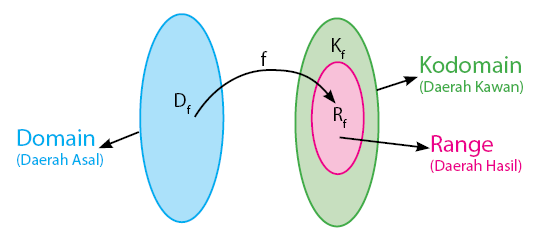
Domain, Kodomain dan Range

Perlu kalian ketahui, dalam konteks fungsi dari himpunan A ke himpunan B, maka himpunan A disebut Daerah Asal atau Domain dan himpunan B disebut dengan Daerah Kawan atau Kodomain. Sedangkan himpunan bagian dari himpunan B yang semua anggotanya mendapat pasangan di anggota himpunan A disebut Daerah Hasil atau Range. 

Contoh: 

Tentukan domain, kodomain dan range dari diagram panah berikut!

Jawab:

A={1, 2, 3, 4, 5} merupakan daerah asal (domain)

B={a, b. c, d, e} merupakan daerah kawan (kodomain)

{a, c, e} disebut daerah hasil (range) yaitu himpunan anggota-anggota B yang mempunyai pasangan dengan anggota A

dari contoh diatas 1 dipasangkan dengan a, dapat ditulis 1 → a, dibaca "1 dipetakan ke a". Pada bentuk 1 → a, a disebut bayangan atau peta dari 1. 

Untuk penamaan suatu fungsi (pemetaan) dapat diberi nama dengan f, g, h atau huruf kecil lainnya, misalnya :

• f : A → B dibaca "fungsi f memetakan A ke B"
• g : 1 → a dibaca "fungsi g memetakan 1 ke a"
• h : 5 → e dibaca "fungsi h memetakan 5 ke e"

Menyatakan Fungsi

Pada bahasan diatas telah telah dikemukakan bahwa fungsi adalah relasi khusus. Oleh karena itu, fungsi oun dapat dinyatakan dengan cara-cara seperti menyatakan relasi, yaitu dengan tiga cara berikut

1. diagram panah

2. diagram kartesius

3. himpunan pasangan berurutan

4. tabel

untuk memahami cara menyatakan fungsi, pelajari lagi materi sebelumnya pada pembahasan relasi.

Demikian pertemuan kali ini, silahkan kalian pelajari lagi materi diatas sampai benar benar paham jika ada yang tidak dimengerti silahkan tanyakan di kolom komentar. Jika kalian merasa sudah paham silahkan menuju link berikut untuk mengerjakan latihan disini.