LK 1.1
Mapel : Matematika
Materi : Pola Bilangan
Sub Materi : Menentukan Persamaan dari suatu Barisan Bilangan
Kelas : VIII
Assalamualaikum wr wb....




Hallo anak-anak ketemu lagi dalam pelajaran matematika. Kali ini kita akan belajar tentang materi pola bilangan. Silahkan kalian baca terlebih dahulu artikel dibawah kemudian pahami. Baca dengan seksama agar kalian dapat memahami setiap instruksi yang diberikan. Disini bapak juga sudah melampirkan video supaya pemahaman kalian lebih baik lagi.
Selamat Belajar...
1. Matematika Materi 1 : Pola Bilangan
Artikel ini akan membahas cara mencari pola bilangan dan mengetahui perbedaan yang terdapat pada macam-macam pola bilangan.
--
Coba ingat-ingat deh waktu kamu ulang tahun, kue yang diberikan orang tuamu berbentuk apa? Kalau ulang tahun Amar, kue ulang tahunnya berbentuk lingkaran nih,kebetulan kemarin adalah ulang tahun Amar. Acaranya sangat meriah sekali lho, apalagi saat pemotongan kuenya. Ternyata saat acara pemotongan kue, Amar tertarik pada pola pemotongan kuenya. Coba perhatikan pola potongan kue di bawah ini yaa!!!
Sebelum kuenya dipotong, bentuk kuenya masih utuh. Kemudian, setelah potongan pertama bentuk kuenya tinggal ¾. Lalu dipotong lagi menjadi ½. Nah, urutan susunan potongan kue yang teratur tersebut dinamakan pola, Pola tersebut tersusun secara teratur dan tetap. Tahukah kamu kalau pola tersebut termasuk ke dalam materi matematika? Kalau dalam matematika kita mengenalnya dengan pola bilangan. Kira-kira pola selanjutnya untuk pemotongan kue terakhir seperti apa ya, Yuk, prediksi pola selanjutnya apa! Kamu boleh tulis jawabannya di kolom komentar di bawah, ya.
Selanjutnya, kita kenalan dulu yuk dengan Pengertian dan jenis-jenis pola bilangan.
Pengertian Pola Bilangan
Definisi pola bilangan matematika adalah susunan dari beberapa angka yang dapat membentuk pola tertentu. Pola bilangan juga bisa diartikan sebagai suatu susunan bilangan yang memiliki bentuk teratur atau suatu bilangan yang tersusun dari beberapa bilangan lain yang membentuk suatu pola.
Macam Macam Pola Bilangan
1. Pola Bilangan Ganjil
Pengertian pola bilangan ganjil adalah pola bilangan yang terbentuk dari bilangan-bilangan ganjil. Sedangkan pengertian bilangan ganjil adalah suatu bilangan asli yang tidak habis dibagi dua ataupun kelipatannya.
Pola bilangan ganjil adalah 1, 3, 5, 7,……..
Gambar Pola Bilangan Ganjil
Rumus Pola Bilangan ganjil
1 , 3 , 5 , 7 , . . . , n ,
maka rumus pola bilangan ganjil ke n adalah:
Un = 2.n-1
Contoh Soal Pola Bilangan Ganjil
1 , 3 , 5 , 7 , . . . , ke 12.
Berapakah pola bilangan ganjil ke 12 ?
Jawab :
Un = 2.n-1
U12 = 2(12)-1
U12 = 24 -1 = 23
Jadi bilangan pada pola ke 12 adalah 23
2. Pola Bilangan Genap
Pengertian pola bilangan genap adalah pola bilangan yang terbentuk dari bilangan-bilangan genap . Bilangan genap adalah bilangan asli yang habis dibagi dua atau kelipatannya .
Pola bilangan genap adalah 2 , 4 , 6 , 8 , . . .
Gambar Pola Bilangan Genap
2 , 4 , 6 , 8 , . . . . , n
maka rumus pola bilangan genap ke n adalah:
Un = 2n
Contoh Soal Pola Bilangan Genap
2 , 4 , 6 , 8 , . . .
Berapakah pola bilangan genap ke 12 ?
Jawab :
Un = 2n
U12 = 2 (12)
U12 = 24
Jadi bilangan pada pola ke 12 adalah 24
3. Pola Bilangan Persegi
Pengertian pola bilangan persegi adalah suatu barisan bilangan yang membentuk suatu pola persegi .
Pola bilangan persegi adalah 1 , 4 , 9 , 16 , 25 , . . .
Gambar Pola Bilangan Persegi
Rumus Pola Bilangan Persegi
1 , 4 , 9 , 16 , 25 , 36 , . . . , n
maka rumus untuk mencari pola bilangan persegi ke-n adalah:
Un = n2
Contoh Pola Bilangan Persegi
Dari suatu barisan bilangan 1 , 4 , 9 , 16 , 25 , 36 , . . . ,n
Berapakah pola bilangan ke 12 dalam pola bilangan persegi ?
Jawab :
Un = n2
U12 = 122
U12 = 12 x 12 = 244
4. Pola Bilangan Persegi Panjang
Pengertian pola bilangan persegi panjang adalah suatu barisan bilangan yang membentuk pola persegi panjang .
Pola persegi panjang adalah 2 , 6 , 12 , 20 , 30 , . . .
Gambar Pola Bilangan Persegi Panjang
Rumus Pola Bilangan Persegi Panjang
2 , 6 , 12 , 20 , 30 , . . . n ,
maka rumus pola bilangan persegi panjang ke-n adalah:
Un = n (n + 1)
Contoh Soal Pola Bilangan Persegi Panjang
Dari suatu barisan bilangan 2 , 6 , 12 , 20 , 30 , . . . , n
Berapakah pola bilangan persegi ke 12?
Jawab :
Un = n .(n+ 1)
U12 = 12 (12 + 1)
U12 = 12 (13)
U12 = 156
5. Pola Bilangan Segitiga
Pengertian bola bilangan segitiga adalah suatu barisan bilangan yang membentuk sebuah pola bilangan segitiga. Pola bilangan segitiga adalah 1 , 3 , 6 , 10 , 15 , . . .
Gambar Pola Bilangan Segitiga
Rumus Pola Bilangan Segitiga
1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , n .
Maka rumus pola bilangan segitiga ke n adalah:
Un = 1/2 n ( n + 1 )
Contoh Soal Pola Bilangan Segitiga
Dari suatu barisan bilangan 1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , n .
Berapakah pola bilangan segitiga ke 12?
Jawab :
Un = 1/2 n ( n + 1 )
U12 = 1/2 . 12 (12 + 1)
U12 = 6 (13)
U12 = 78
6. Pola Bilangan Fibonacci
Pengertian pola bilangan fibonacci adalah suatu bilangan yang setiap sukunya merupakan jumlah dari dua suku di depannya. Pola bilangan Fibonacci adalah 1, 1, 2, 3, 5, 8, 13, 21, 34, ……
Perlu diketahui, 2 diperoleh dari hasil 1 + 1, 3 diperoleh dari hasil 2 + 1, 5 diperoleh dari hasil 3 + 2, 8 diperoleh dari dari hasil 5 + 3 dan seterusnya.
Rumus mencari suku ke-n pola bilangan fibonacci adalah
Un = Un-1 + Un-2
Gambar Pola Bilangan Fibonacci
Contoh soal pola bilangan fibonacci:
Tentukan dua suku berikutnya dari bilangan berikut
2,2,4,6,10,16,....,....
Jawab:
Suku ke 7
Un = Un-1 + Un-2
U7 = U7-1 + U7-2
U7 = U6 + U5
U7 = 16 + 10
U7 = 26
Suku ke-8
Un = Un-1 + Un-2
U8 = U8-1 + U8-2
U8 = U7 + U6
U8 = 26 + 16
U8 = 42
Jadi dua bilangan selanjutnya dari pola bilangan diatas adalah 26 dan 42.
7. Pola Bilangan Segitiga Pascal
Bilangan pascal ditemukan oleh oleh orang Prancis bernama Blaise Pascal, sehingga dinamakan bilangan pascal. Bilangan pascal adalah bilangan yang terbentuk dari sebuah aturan geometri yang berisi susunan koefisien binomial yang bentuknya menyerupai segitiga.
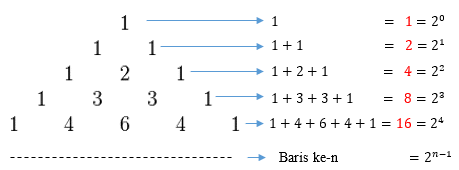
Di dalam segitiga pascal, bilangan yang terdapat pada satu baris yang sama dijumlahkan menghasilkan bilangan yang ada di baris bawahnya. Jadi, pengertian pola bilangan pascal adalah suatu pola yang tersusun dari beberapa angka berdasarkan rumus.
Gambar Pola Bilangan Pascal

Pola bilangan pascal adalah 1, 2, 4, 8, 16, 24, 32, 64,…..
Rumus pola bilangan pascal :
Un = 2 n-1
Contoh soal pola bilangan pascal:
Tentukan suku ke 12 pola bilangan pascal:
jawab:
U12 = 2 12-1
U12 = 2 11
U12 = 2048
Jadi jumlah bilangan pada baris ke -12 pada segitiga pascal adalah 2048.
Itulah sebagian contoh pola bilangan yang dapat dituliskan. Sebenarnya masih banyak pola bilangan yang tidak dituliskan diatas tetapi kita kalian diharapkan mampu untuk mengidentifikasi besar bilangan pada suku yang ditanyakan.
Perhatikan contoh soal berikut!
Pada contoh di atas, kamu diperintahkan untuk menentukan suku ke 5 dan 6. Jadi, langkah pertama kamu harus melihat dulu pola dari bilangan-bilangan sebelumnya. Coba kamu lihat selisih dari tiap bilangannya. Selisih dari bilangan pertama ke bilangan kedua adalah 5. Selanjutnya selisih dari bilangan kedua ke bilangan ketiga adalah 6, dan begitu seterusnya. Ternyata selisihnya selalu bertambah satu. Langkah kedua yaitu kamu harus melakukan operasi yang sama dengan pola yang tadi telah ditemukan. Jadi, untuk menentukan bilangan yang ke-5, kamu harus menambahnya dengan angka 8, sehingga 23 + 8 = 31. Sedangkan untuk menentukan suku ke 6, kamu harus menambahnya dengan angka 9. Jadi, 31 + 9 = 40. Mudahkan?
untuk lebih memperkuat pemahaman kita terhadap materi pola bilangan kalian dapat melihat video berikut
Demikian artikel ini semoga dapat membantu kalian dalam menyelesaikan soal-soal yang berhubungan dengan materi pola bilangan.




No comments:
Post a Comment