Sistem Persamaan Linier Dua Variabel (SPLDV) Part 1
LK-5.1
Mapel : Matematika
Materi : Sistem Persamaan Linier Dua Variabel
Sub Materi : Persamaan Linier Dua Variabel
Kelas : VIII
Hari/Tanggal : Senin, 18 Januari 2021
Assalamualikum wr wb...
Selamat pagi semuanya, sekarang bertemu lagi dengan bapa pada mata pelajaran matematika, alhamdulillah sekarang kita sudah menginjak semester genap, walaupun masih belajar dalam moda seperti ini mudah-mudahan tidak mengurangi semangat kalian dalam belajar. amiin
Kemudian marilah kita berdoa semoga pandemi covid-19 ini dapat segera hilang dari dunia ini sehingga kita dapat melaksanakan segala kegiatan kita sebagaimana mestinya.
Pada pertemuan kali ini kita akan belajar tentang Sistem Persamaan Linier Dua Variabel (SPLDV). Bacalah materi berikut dengan seksama kemudian kerjakan latihannya agar kalian dapat lebih mengerti.
A. Persamaan Linier Dua Variabel (PLDV)
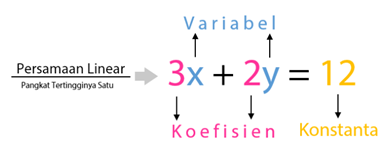
Sebelum ke pembahasan sistem persamaan linear dua variabel, kenali terlebih dahulu apa itu persamaan linear? Sebuah persamaan linear memiliki komponen yang meliputi variabel, koefisien, dan konstanta. Variabel adalah nilai yang dapat berubah – ubah. Koefisien adalah bilangan yang berada di depan variabel. Satu lagi, konstanta adalah bilangan yang tidak diikuti oleh variabel.
B. Pengertian Sistem Persamaan Linear Dua Variabel (SPLDV)
Sistem persamaan linear dua variabel adalah dua persamaan linear dua variabel yang mempunyai hubungan diantara keduanya dan mempunyai satu penyelesaian.
Apabila terdapat dua persamaan linear dua variabel yang berbentuk ax + by = c dan dx + ey = f atau biasa ditulis
Maka dikatakan dua persamaan tersebut membentuk sistem persamaan linear dua variabel. Penyelesaian sistem persamaan linear dua variabel tersebut adalah pasangan bilangan (x, y) yang memenuhi kedua persamaan tersebut.
C. Penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV)
Untuk menentukan penyelesaian atau akar dari Sistem Persamaan Linear Dua Variabel, dapat ditentukan dengan tiga cara yaitu :
• Metode Grafik
• Metode Substitusi
• Metode Eliminasi
1. Metode Grafik
Langkah – langkah menyelesaikan SPLDV dengan metode grafik :
• Tentukan nilai koordinat titik potong masing-masing persamaan terhadap sumbu-X dan juga sumbu-Y
• Gambarkan grafik dari masing-masing persamaan pada sebuah bidang Cartesius
• Jika kedua garis berpotongan pada satu titik, maka himpunan penyelesaiannya tepat memiliki satu anggota.
Contoh 1 :
Tentukan himpunan penyelesaian dari persamaan berikut ini :
Persamaan 1 : x + y = 5
Persamaan 2 : x − y = 1
Jawab:
Langkah Pertama, Tentukan titik potong sumbu-x dan sumbu-y
Titik Potong Persamaan 1 yaitu x + y = 5
Menentukan titik koordinat jika y = 0
x + y = 5
x + 0 = 5 ---> y diganti 0 karena syaratnya y=0
x = 5
Maka titik koordinatnya (5,0)
Menentukan titik koordinat jika x = 0
x + y = 5
0 + y = 5 ---> x diganti 0 karena syaratnya x=0
y = 5
Maka titik koordinatnya (0,5)
Titik Potong untuk Persamaan 2 yaitu x – y = 1
Menentukan titik potong sumbu-x maka syaratnya y = 0
x – y = 1
x – 0 = 1 ---> y diganti 0 karena syaratnya y=0
x = 1
Maka titik koordinatnya (1,0)
Menentukan titik potong sumbu-y maka syaratnya x = 0
x – y = 1
0 – y = 1 ---> x diganti 0 karena syaratnya x=0
y = -1
Maka titik koordinatnya (0,-1)
Langkah Kedua, Gambarkan grafik dari masing – masing titik potong dari kedua persamaan diatas. Maka hasilnya dapat dilihat digambar dibawah ini

Dilihat dari gambar grafik di atas, maka titik potong dari kedua grafik diatas adalah di titik (3, 2).Maka hasil dari Himpunan Penyelesaian adalah {3,2}
Contoh 2:
Dengan metode grafik, tentukan himpunan penyelesaian sistem persamaan linear dua variabel x + y = 5 dan x – y = 1,. Jika x, y variabel pada himpunan bilangan real.
Jawab:
Buatlah garis untuk menentukan titik potong kedua persamaan
Persamaan 1 : x + y = 5
Menentukan titik koordinat jika y = 0
Maka titik koordinatnya (5,0)
Menentukan titik koordinat jika x = 0
Maka titik koordinatnya (0,5)
Persamaan 2 : x – y = 1
Menentukan titik koordinat jika y = 0
Maka titik koordinatnya (1,0)
Menentukan titik koordinat jika x = 0
x - y = 1
0 - y = 1
-y = 1
y=-1
Maka titik koordinatnya (0, -1)
Kemudian gambar pada bidang koordinat kartesius seperti tampak pada gambar berikut
Dari gambar tampak bahwa koordinat titik potong kedua garis adalah (3, 2). Jadi, himpunan penyelesaian dari sistem persamaan x + y = 5 dan x – y = 1 adalah {(3,2)}.
Contoh 3 :
Tentukan himpunan penyelesaian dari sistem persamaan x + 2y=2 dan 2x + 4y=8 untuk x, y ∈ R menggunakan metode grafik.
Jawab:
Buatlah garis untuk menentukan titik potong kedua persamaan
Persamaan 1 : x + 2y=2
Menentukan titik koordinat jika y = 0
x + 2y = 2
x + 2(0) = 2
x + 0 = 2
x = 2
Maka titik koordinatnya (2,0)
Menentukan titik koordinat jika x = 0
x + 2y = 2
0 + 2y = 2
2y = 2
y = 2/2
y = 1
Maka titik koordinatnya (0,1)
Persamaan 2 : 2x + 4y = 8
Menentukan titik koordinat jika y = 0
2x + 0 = 8
2x = 8
x = 8/2
x = 4
Maka titik koordinatnya (4,0)
Menentukan titik koordinat jika x = 0
0 + 4y = 8
4y = 8
y = 8/4
y = 2
Maka titik koordinatnya (0,2)
kita gambarkan grafik dari masing-masing persamaan pada sebuah bidang Cartesius seperti yang ditunjukkan pada gambar di bawah ini.
Berdasarkan gambar grafik sistem persamaan di atas, tampak bahwa kedua garis tersebut tidak akan pernah berpotongan karena keduanya sejajar. Dengan demikian, himpunan penyelesaian dari sistem persamaan x + 2y = 2 dan 2x + 4y = 8 adalah himpunan kosong, ditulis {} atau {∅}
Jika kalian perhatikan, penggunaaan metode grafik untuk menyelesaikan SPLDV kelihatannya memang cukup mudah dan efektif, akan tetapi metode grafik memiliki kelemahan yaitu ketika digunakan untuk menentukan himpunan penyelesaian di mana titik potong terjadi pada koordinat berupa pecahan, tentu kalian akan merasa kesulitan. Oleh karena itu kita dapat menggunakan beberapa metode alternatif lainnya misalnya dengan menggunakan metode eliminasi atau substitusi atau gabungan dari keduanya. Seperti apa penggunaan metode eliminasi dan substitusi kita akan pelajari pada pertemuan selanjutnya.
Demikian materi untuk hari ini semoga kalian semua dapat memahami materi yang diberikan dan jangan lupa kerjakan tugasnya di bawah.
Tugas 5.1
Dengan metode grafik tentukanlah himpunan penyelesaian dari sistem persamaan 2x + y = 6 dan 2x + 4y = 12
Petunjuk Pengisian
1. Kerjakan dalam buku tugas Matematika
2. Cantumkan nomor tugas dan Tanggal Pengerjaan
3. Cantumkan Nama lengkap dan Kelas
4. Kerjakan sesuai dengan instruksi soal.
5. Foto tugas yang telah kalian buat dengan jelas dan tidak blur.




No comments:
Post a Comment