Agus Maulana Idrus, S.Pd: Teorema Pythagoras Part 1

LK-6.1

Mapel : Matematika

Materi : Teorema Pythagoras

Sub Materi : Pembuktian dan Rumus Teorema Pythagoras

Kelas : VIII

Hari/Tanggal : Senin, 15 Februari 2021

Assalamualikum wr wb...

Selamat pagi semuanya, sekarang bertemu lagi dengan mata pelajaran matematika. Bagaimana Keadaan kalian saat ini? Bapa doakan semoga kalian semuanya sehat selalu

Sebelum mulai marilah kita berdoa semoga pandemi covid-19 ini dapat segera berakhir sehingga kita dapat melaksanakan segala kegiatan kita sebagaimana mestinya.

Alhamdulillah kita telah selesaikan materi sebelumnya yaitu SPLDV, sekarang kita lanjutkan ke materi selanjutnya yaitu tentang Teorema Phytagoras. Pada pertemuan kali ini kita akan membahas tentang Pembuktian dan Rumus Teorema Phytagoras. Apa dan bagaimana Teorema Phytagoras itu? coba kalian baca materi berikut dengan baik agar kalian memperoleh pemahaman yang sempurna. Kemudian kerjakan latihannya agar kalian dapat lebih mengerti.

1. Definisi Pythagoras
Pythagoras merupakan salah satu teorema atau aturan dalam matematika yang membahasa mengenai keterkaitan sisi-sisi segitiga, dalam hal ini merupakan segitiga siku-siku. Teorema ini pertama kali dikemukakan oleh seorang matematikiawan yang berasal dari Yunani bernama Phytagoras.

2. Penerapan Pythagoras
Contoh penerapan pythagoras dapat dilihat pada bidang pertukangan. Tukang bangunan biasanya menggunakan penggaris siku untuk menentukan bahwa sudut yang dibentuk oleh pondasi bangunan merupakan sudut siku-siku. Selain itu, tukang biasanya juga membuat kerangka atap yang menerapkan konsep pythagoras. Selain itu juga untuk menentukan jarak terdekat dari dua posisi dapat dengan mudah ditentukan menggunakan teorema pythagoras. Selanjutnya akan dijelaskan mengenai teorema pythagoras.

3. Teorema Pythagoras

Teorema pythagoras menyatakan bahwa kuadrat sisi miring segitiga siku-siku (hipotenusa) sama dengan jumlah kuadrat sisi-sisi yang saling berpenyiku. Atau secara sederhana dapat dijelaskan bahwa jika sisi terpanjang segitiga siku-siku dikuadratkan maka akan sama dengan jumlah dari kuadrat sisi yang lainnya.

4. Rumus Pythagoras

Dari pembuktian di atas dapat dirumuskan teorema pythagoras sebagai berikut. Misalkan terdapat segitiga siku-siku dengan ukuran sisi masing-masing adalah a, b, dan c.

Teorema Phytagoras sendiri seperti yang telah dissebutkan di atas merupakan teorema yang menerangkan tentang hubungan antara sisi-sisi yang ada dalam sebuah segitiga siku-siku.

Adapun bunyi atau dalil Teorema Phytagoras yaitu sebagai berikut: Pada suatu segitiga siku-siku, kuadrat dari sisi terpanjang yaitu sama dengan hasil jumlah dari kuadrat sisi-sisi penyikunya.

Dari teorema tersebut bisa kita buat suatu rumus yang bisa kita gambarkan seperti di bawah ini:

Sebagai contoh, diketahui sebuah segitiga dengan siku-siku di C. Apabila panjang sisi miring (hipotenusa) yaitu c serta panjang sisi-sisi penyikunya (sisi selain sisi miring) yaitu a dan b. Maka teorema Phytagoras di atas bisa kita rumuskan seperti berikut ini:

Rumus Phytagoras

c² = a² + b²

Keterangan:

c = sisi miring

a = tinggi

b = alas

Rumus Phytagoras pada umumnya dipakai dalam mencari panjang sisi miring segitiga siku-siku seperti berikut ini:

Kuadrat sisi AB = kuadrat sisi AC + kuadrat sisi BC. atau AB² = AC² + BC² atau c² = a² + b²

Rumus untuk mencari panjang sisi alas yaitu:

b² = c² – a²

Rumus untuk mencari sisi samping atau tinggi segitiga yaitu:

a² = c² – b²

Rumus untuk mencari sisi miring segitiga siku-siku yaitu:

c² = a² + b²

Contoh Soal Pythagoras

Soal 1.
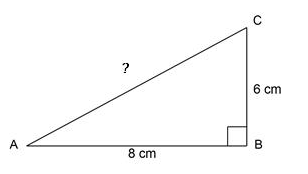
Diketahui segitiga siku-siku ABC dengan siku-siku di B yang digambarkan sebagai berikut:

Tentukan panjang sisi miring AC pada gambar di atas!
Jawab:
Sebab segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti betikut ini:
AC² = AB² + BC²
AC² = 8² + 6²
AC² = 64 + 36
AC² = 100
AC = √100
AC = 10
Sehingga, panjang sisi AC dalam segitiga siku-siku tersebut yaitu 10 cm.

Soal 2.
Suatu segitiga siku-siku KLM dengan siku-siku di L digambarkan seperti di bawah ini:

Tentukan panjang sisi KL pada gambar di atas!
Jawab:
Sebab, segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti berikut ini:
KM² = KL² + LM²
KL² = KM² – LM²
KL² = 13² – 12²
KL² = 169 – 144
KL² = 25
KL = √25
KL = 5
Sehingga, panjang sisi KL dalam segitiga siku-siku di atas yaitu 5 cm.

Soal 3.
Diketahui segitiga siku-siku DEF dengan siku-siku di E digambarkan seperti di bawah ini:

Tentukan panjang sisi DE pada gambar di atas!
Jawab:
Sebab segitiga DEF di atas merupakan segitiga siku-siku, maka berlaku rumus Phytagoras seperti di bawah ini:
DF² = DE² + EF²
DE² = DF² – EF²
DE² = 15² – 9²
DE² = 225 – 81
DE² = 144
DE = √144
DE = 12
Sehingga, panjang sisi DE pada segitiga siku-siku di atas yaitu 12 cm.

Soal 4.
Diketahui segitiga siku-siku ABC dengan siku-siku berada di B. Apabila panjang sisi AB = 16 cm serta Panjang sisi BC = 12 cm.
Maka hitunglah panjang sisi AC !
Jawab:
Dari soal di atas bisa kiat gambarkan sebuah segitiga siku-siku seperti berikut ini:

Sebab segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti di bawah ini:
c² = a² + b²
c² = 12² + 16²
c² = 144 + 256
c² = 400
c = √400
c = 20
Sehingga, panjang sisi AC pada segitiga siku-siku ABC dalam soal di atas yaitu 20 cm.

Agar Kalian dapat lebih mengerti silahkan simak video berikut https://www.youtube.com/watch?v=rHT17HtmoaU .

Setelah kalian mempelajari materi diatas, selanjutnya silahkan kalian kerjakan latihan berikut. Jika ada yang tidak dimengerti silahkan berkomentar di bawah atau tanyakan langsung via WhatsApp.

Tugas 6.1

Kerjakan Soal-Soal Berikut dengan Baik dan Benar!

1. Diberikan sebuah segitiga siku-siku pada gambar berikut ini: