Teorema Pythagoras Part 4

 LK-6.4

Mapel               : Matematika

Materi               : Teorema Pythagoras

Sub Materi       : Perbandingan Sisi-Sisi Segitiga Siku-Siku Khusus

Kelas                 : VIII

Hari/Tanggal  : Kamis, 25 Februari 2021

Assalamualikum wr wb...

Selamat pagi semuanya, sekarang bertemu lagi dengan mata pelajaran matematika. Bagaimana Keadaan kalian saat ini? Bapa doakan semoga kalian semuanya sehat selalu

Sebelum mulai marilah kita berdoa semoga pandemi covid-19 ini dapat segera berakhir sehingga kita dapat melaksanakan segala kegiatan kita sebagaimana mestinya.

Pada pertemuan kali ini kita akan membahas tentang Menentukan Jenis Segitiga. Silahkan kalian baca materi berikut dengan baik agar kalian memperoleh pemahaman yang sempurna. Kemudian kerjakan latihannya agar kalian dapat lebih mengerti

5. Perbandingan Sisi-Sisi Segitiga Siku-Siku Khusus

Masih ingatkah Kalian dengan cara membuktikan Teorema Pythagoras dan cara mencari salah satu sisi segitiga siku-siku jika kedua sisi yang lainnya diketahui? Selain bisa digunakan untuk mencari salah satu sisi segitiga siku-siku, teorema Pythagoras bisa digunakan untuk mencari perbandingan sisi-sisi pada segitiga siku-siku pada sudut khusus. Adapun sudut khusus yang dimaksud di sini adalah 30°, 45°, dan 60°. Bagaimana perbandingan sisi-sisi pada segitiga siku-siku pada sudut khusus?

1. Segitiga Siku-Siku yang Slah Satu Sudutnya 30° atau 60°

Perhatikan gambar berikut!

∆ABC adalah segitiga sama sisi dan CD adalah garis tingginya. 

Panjang AB = BC = AC,

Besar ∠ACB = ∠A = ∠B = 60° 

Besar ∠ACD = ∠BCD = 30°

AD = BD = ½ AB, atau

AD = BD = ½ BC, sebab BC = AB

AD = BD = ½ AC, atau AC = AB

Jika Segitiganya kita pisah maka diperoleh segitiga berikut

Besar ∠BCD = 30° dan besar ∠CBD = 60°

Panjang BD = ½ BC

Dalam setiap Segitiga Siku- Siku yang besar salahsatu sudutnya 30°, maka panjang sisi dihadapan sudut 30° adalah ½ sisi miring.

dari gambar diatas jika panjang BC = 2 satuan, maka panjang BD dan CD dapat dihitung dengan cara berikut

BD = ½ BC

BD = ½ (2)

BD = 1

Jadi panjang BD adalah 1 satuan

Untuk mencari panjang CD dapat digunakan teorema pythagoras

CD² = BC² - BD²

CD² = 2²  - 1²

CD² = 4 - 1

Cd² = 3

CD = √3

Berdasarkan hasil diatas dapat disusun perbandingan sebagai berikut:

Contoh:

pada gambar disamping, ∆ABC siku-siku di A dengan panjang BC = 6 cm dan besar ∠B = 30°. 

Hitunglah:

a. Panjang AB

b. Panjang AC

Jawab:

a. BC : AB = 2 : √3

Jadi Panjang AB adalah 3√3 cm.

2. Segitiga Siku-Siku yang Slah Satu Sudutnya 45°

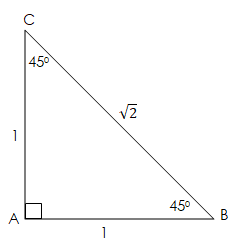
Sekarang perhatikan gambar di bawah ini!

 ∆ABC adalah segituga siku-siku samakaki, sehingga:

Panjang AB = Panjang AC dan besar ∠ABC = ∠ABC = 45°. 

Maka pada gambar diatas berlaku perbandingan 

AB : AC : BC = 1 :1 : √2

Contoh :

Diketahui  ∆ABC siku-siku dengan panjang AB = 4cm dan besar sudut ∠B = 45°. Hitunglah panjang AC dan BC!

Jawab:

Panjang AB = Panjang BC

Panjang 4 cm jadi panjang AC = 4 cm

Jadi Panjang AC adalah 4 cm dan panjang BC = 4√2 cm

Baca kembali materi diatas sampai kalian mampu memahaminya kemudian kerjakan tugas di bawah ini

Tugas 6.4

1. pada persegi panjang PQRS di samping,

panjang diagonal QS = 12 cm, dan besar ∠PSQ = 60°. Hitunglah

a. panjang PQ

b. Panjang QS 

2. Diketahui ∆PQR siku-siku dengan panjang PQ = 12 cm.

hitunglah panjang QR dan panjang PQ !

Petunjuk Pengisian

1. Kerjakan dalam buku tugas Matematika

2. Cantumkan nomor tugas dan Tanggal Pengerjaan

3.    Cantumkan Nama lengkap dan Kelas

4.    Kerjakan sesuai dengan instruksi soal.

5.    Foto tugas yang telah kalian buat dengan jelas dan tidak blur.

6.    Kemudian upload fotonya dengan cara  >> KLIK DISINI<<