Teorema Pythagoras Part 3

 LK-6.3

Mapel               : Matematika

Materi               : Teorema Pythagoras

Sub Materi       : Menentukan Jenis Segitiga

Kelas                 : VIII

Hari/Tanggal  : Senin, 22 Februari 2021

Assalamualikum wr wb...

Selamat pagi semuanya, sekarang bertemu lagi dengan mata pelajaran matematika. Bagaimana Keadaan kalian saat ini? Bapa doakan semoga kalian semuanya sehat selalu

Sebelum mulai marilah kita berdoa semoga pandemi covid-19 ini dapat segera berakhir sehingga kita dapat melaksanakan segala kegiatan kita sebagaimana mestinya.

Pada pertemuan kali ini kita akan membahas tentang Menentukan Jenis Segitiga. Silahkan kalian baca materi berikut dengan baik agar kalian memperoleh pemahaman yang sempurna. Kemudian kerjakan latihannya agar kalian dapat lebih mengerti.

D. Menentukan Jenis Segitiga

Dengan menggunakan kebalikan teorema pythagoras, jika sisi-sisi suatu segitiga diketahui panjangnya, maka kita dapat memerikasa apakah segitiga tersebut merupakan segitiga siku-siku atau bukan

Selanjutnya, jika suatu segitiga tidak siku-siku, maka kita dapat menentukan apakah segitiga itu merupakan segitiga lancip atau segitiga tumpul. untuk melakukan pengerjaan ini, kembali kita gunakan kebalikan teorema pythagoras.

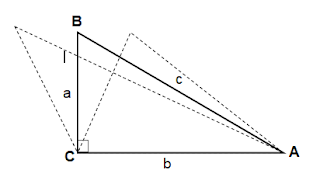
Perhatikan Segitiga di bawah

Dalam segitiga ABC dengan panjang sisi a, b dan c, berlaku

* jika a² < b²  + c² , maka segitiga ABC adalah segitiga lancip. Sisi a terletak dihadapan sudut A dan a merupakan sisi terpanjang

*  jika a² = b²  + c² , maka segitiga ABC adalah segitiga siku-siku. Sisi a terletak dihadapan sudut A dan a merupakan sisi terpanjang

* jika a² > b²  + c² , maka segitiga ABC adalah segitiga tumpul. Sisi a terletak dihadapan sudut A dan a merupakan sisi terpanjang

Contoh 1

Suatu segitiga berukuran 4cm, 3cm dan 5cm. Tentukanlah jenis segitiga tersebut lancip, siku-siku atau segitiga tumpul.

jawab:

misalkan sisi terpanjang adalah a, maka:

a=5 cm, b=4cm dan c=3cm

a² = 5² = 25

b²+c² = 4² +3² = 16 + 9 = 25

karena  a² = b²  + c², maka segitiga tersebut adalah segitiga siku-siku.

Contoh 2

segitiga berukuran 7cm, 9cm dan 10cm. Apakah segitiga tersebut merupakan segitiga siku-siku?

jawab:

misalkan sisi tepanjang adalah a, maka:

a=10cm, b=7cm dan c=9cm

a² = 10² = 100

b²+c² = 7² + 9² 

           = 49 + 81 

           = 130

karena  a² ≠ b²  + c², maka segitiga tersebut bukan segitiga siku-siku

Nilai a² < b²  + c², maka segitiga tersebut adalah segitiga lancip

Kebalikan Teorema Pythagoras

Jika pada segitiga ABC berlaku hubungan:
$1.{\mathrm{a²\; =\; b² \; +\; c²}}^{}$, maka segitiga ABC siku-siku di A.
$2.{\mathrm{b²\; =\; a² \; +\; c²}}^{}$, maka segitiga ABC siku-siku di B.
$3.{\mathrm{c²\; =\; a² \; +\; b²}}^{}$, maka segitiga ABC siku-siku di C.

$4.{\mathrm{a²\; <\; b² \; +\; c²}}^{}$, maka segitiga ABC merupakan segitiga lancip di A.
$5.{\mathrm{b²\; <\; a² \; +\; c²}}^{}$, maka segitiga ABC merupakan segitiga lancip di B.
$6.{\mathrm{c²\; <\; a² \; +\; b²}}^{}$, maka segitiga ABC merupakan segitiga lancip di C.

$7.{\mathrm{a²\; >\; b² \; +\; c²}}^{}$, maka segitiga ABC merupakan segitiga tumpul di A.
$8.{\mathrm{b²\; >\; a² \; +\; c²}}^{}$, maka segitiga ABC merupakan segitiga tumpul di B.
$9.{\mathrm{c²\; >\; a² \; +\; b²}}^{}$, maka segitiga ABC merupakan segitiga tumpul di C.

Setelah kalian mempelajari materi diatas kalian kerjakan latihan berikut.

Tugas 6.3

Perhatikan segitiga dibawah ini!

Pada segitiga DEF diatas.  Panjang DG =  9 cm, GE = 16 cm dan FG = 12 cm. Hitunglah

a. Panjang DF

b. Panjang EF

c. Jenis segitiga DEF. (Siku-Siku, Lancip, Tumpul)

Petunjuk Pengisian

1. Kerjakan dalam buku tugas Matematika

2. Cantumkan nomor tugas dan Tanggal Pengerjaan

3.    Cantumkan Nama lengkap dan Kelas

4.    Kerjakan sesuai dengan instruksi soal.

5.    Foto tugas yang telah kalian buat dengan jelas dan tidak blur.

6.    Kemudian upload fotonya dengan cara  >> KLIK DISINI<<