LK. 7.3
Mapel : Matematika
Materi : Bangun Ruang Sisi Datar
Sub Materi : Kubus
Kelas : VIII
Hari/Tanggal : Senin, 5 April 2021
Assalamualikum wr wb...
Selamat pagi semuanya, sekarang bertemu lagi dengan mata pelajaran matematika. Bagaimana Keadaan kalian saat ini? Bapa doakan semoga kalian semuanya sehat selalu
Sebelum mulai marilah kita berdoa semoga pandemi covid-19 ini dapat segera berakhir sehingga kita dapat melaksanakan segala kegiatan kita sebagaimana mestinya.
Baiklah Untuk Pertemuan sekarang kita akan belajarmelanjutkan materi sebelumnya yaitu tentang Kubus dan Balok.
3. Kubus
a. Pengertian Kubus
Kubus merupakan suatu bangun ruang tiga dimensi yang dibatasi oleh enam sisi serupa yang berwujud bujur sangkar.
Kubus juga dikenal dengan nama lain yaitu bidang enam beraturan. Kubus sebetulnya adalah bentuk khusus dari prisma segiempat, sebab tingginya sama dengan sisi alas.
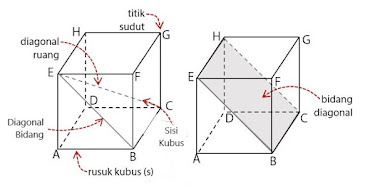
b. Bagian-bagian Kubus
1. Sisi kongruen ada sebanyak 6 buah yang terdiri atas:
* bidang alas kubus: ABCD
* bidang atas kubus: EFGH
*sisi tegak kubus: ABEF, CDGH, ADEH, dan BCFG
* Rusuk sama panjang ada sebanyak 12 buah (AB = BC = CD = DA = EF = FG = GH = HE = AE = BF = CG = DH).
2. Titik sudut berjumlah 8 titik (A, B, C, D, E, F, G, H).
* bidang alas kubus: ABCD
* bidang atas kubus: EFGH
*sisi tegak kubus: ABEF, CDGH, ADEH, dan BCFG
* Rusuk sama panjang ada sebanyak 12 buah (AB = BC = CD = DA = EF = FG = GH = HE = AE = BF = CG = DH).
2. Titik sudut berjumlah 8 titik (A, B, C, D, E, F, G, H).
3. Diagonal bidang yang sama panjang sebanyak 6 buah (AC = BD = EG = FH = AF = BE = CH = DG = AH = DE = BG = CF).
4. Diagonal ruang yang sama panjang sebanyak 4 buah (AG = BH = CE = DF).
5. Bidang diagonal kongruen berjumlah 6 buah (ABGH, EFCD, BCHE, FGDA, BFHG, dan AEGC).
c. Sifat bangun Kubus
1. Seluruh sisi kubus berbentuk persegi dengan mempunyai luas yang sama.
2. Seluruh rusuk kubus memiliki panjang yang sama.
3. Masing-masing diagonal bidang pada kubus mempunyai panjang yang sama.
Perhatikan ruas garis BG dan CF pada gambar di atas. Kedua garis tersebut adalah diagonal bidang kubus ABCD.EFGH yang mempunyai ukuran sama panjang.
4. Masing-masing diagonal ruang pada kubus memiliki panjang yang sama.
Dari kubus ABCD.EFGH pada gambar di atas , ada dua diagonal ruang, yakni HB dan DF di mana keduanya berukuran sama panjang.
5. Masing-masing bidang diagonal pada kubus berbentuk persegi panjang.
Perhatikan bidang diagonal ACGE pada gambar di atas.
d. Jaring Jaring Kubus
Jika kubus dipotong berdasarkan rusuk-rusuknya, lalu masing-masing sisinya direntangkan maka akan menghasilkan suatu bangun datar yang disebut sebagai jaring-jaring kubus.
Terdapat sebelas macam jaring-jaring kubus di mana susunannya berbeda satu sama lain. Masing-masing terdiri atas enam buah persegi kongruen yang saling berkaitan.
Simak gambar yang ada di bawah ini:
e. Rumus Pada Kubus
Contoh Soal
Perhatikan Gambar kubus berikut ini!
a. Volume Kubus
b. Luas permukaan Kubus
c. Panjang diagonal bidang
d. Panjang diagonal ruang
e. Luas bidang diagonal
Jawab :
a. Volume Kubus =s³ = s x s x s = 9 x 9 x 9 = 729 cm³
b. Luas permukaan Kubus = 6s² = 6(9²) = 6 x 81 = 486 cm²
c. Panjang diagonal bidang = s√2 = 9√2 cm
d. Panjang diagonal ruang = s√3 = 9√3 cm
e. Luas bidang diagonal = s2√2 = 9 x 2√2 =18√2 cm
4. Balok
a. Pengertian Balok
Balok adalah suatu bangun ruang yang mempunyai tiga pasang sisi segi empat. Di mana pada masing-masing sisinya yang berhadapan mempunyai bentuk serta ukuran yang sama.
Berbeda halnya dengan kubus di mana seluruh sisinya kongruen berbentuk persegi, dan pada balok hanya sisi yang berhadapan yang sama besar.
Serta tidak seluruhnya berbentuk persegi, kebanyakan berbentuk persegi panjang.
b. Bagian-bagian Balok
Pada masing-masing dari bangun ruang sisi datar yang satu ini sama seperti yang ada pada kubus.
Suatu balok terdiri tas sisi, sudut, diagonal bidang, diagonal ruang, serta yang terakhir yaitu bidang diagonal.
Berikut akan adalah rincian jumlahnya untuk kalian semua:
1. Sisi berbentuk persegi dan juga persegi panjang sebanyak 6 buah, antara lain yaitu:
bidang alas kubus: ABCD
bidang atas kubus: EFGH
sisi tegak kubus: ABEF, CDGH, ADHE, dan BCGF.
2. Rusuk sebanyak 12 buah yang dapat dibagi menjadi 3 kelompok, antara lain:
Panjang (p) yakni rusuk terpanjang dari alas balok serta rusuk lainnya yang sejajar: AB, DC, EF dan HG
lebar (l) adalah rusuk terpendek dari alas balok dan juga rusuk lainnya yang sejajar: BC, AD, FG, dan EH
Tinggi (t) adalah rusuk yang tegak lurus terhadap panjang dan lebar balok: AE, BF, CG, dan DH.
3. Titik sudut berjumlah 8 titik (A, B, C, D, E, F, G, H).
4. Diagonal bidang sebanyak 6 buah (AC, BD, EG, FH, AF, BE, CH, DG, AH, DE, BG, dan CF).
5. Diagonal ruang yang berjumlah 4 buah (AG, BH, CE, dan DF).
6. Bidang diagonal yang berbentuk persegi panjang dengan jumlah 6 buah, antara lain: ABGH, EFCD, BCHE, FGDA, BFHG, dan AEGC.
c. Sifat - Sifat Balok
1. Sedikitnya sebuah balok mempunyai dua pasang sisi yang berbentuk persegi panjang.
2. Rusuk-rusuk yang sejajar memiliki ukuran yang sama panjang:
AB = CD = EF = GH, dan AE = BF = CG = DH.
3. Pada masing-masing diagonal bidang pada sisi yang berhadapan berukuran sama panjang, yakni:
ABCD dengan EFGH, ABFE dengan DCGH, dan BCFG dengan ADHE yang mempunyai ukuran sama panjang.
4. Masing-masing diagonal ruang pada balok mempunyai ukuran sama panjang.
5. Masing-masing bidang diagonalnya berbentuk persegi panjang.
d. Jaring Jaring Balok
Sama halnya dengan kubus, jaring-jaring pada bangun balok juga didapatkan dengan cara membuka balok tersebut sehingga akan terlihat semua permukaan balok.
Jaring-jaring balok lebih banyak apabila dibandingkan dengan jaring-jaring pada kubus. Hal tersebut disebabkan selain persegi sisi-sisi pada balok juga terdiri atas persegi panjang.
Sehingga hasil dari jaring-jaringnya menjadi lebih variatif.
Berikut adalah beberapa contoh dari jaring-jaring balok.
Perhatikan gambar balok di bawah ini!
Jika panjang balok diatas mempunyai panjang 12cm, lebar 5 cm dan tinggi 9 cm. Hitunglah
a. Luas Balok
b. Volume Balok
c. Panjang AF
d. Panjang AC
e. Panjang AG
Jawab:
a. Luas Balok
L = 2(pl + pt + lt)
L = 2(12.5 + 12.9 + 5.9)
L = 2(60 + 108 + 45)
L = 2(213)
L = 416 cm
b. Volume Balok
V= p.l.t
V= 12. 5. 9
V=540 cm³
c. Panjang AF
Gunakan teorema pythagoras
AF² = AB² + BF²
AF² = 12² + 9 ²
AF² = 144 + 81
AF² = 225
AF = √225
AF = 15 cm
d. Panjang AC
Gunakan teorema pythagoras
AC² = AB² + BC²
AC² = 12² + 5²
AC² = 144 + 25
AC² = 169
AC = √169
AC = 13 cm
e. Panjang AG
Gunakan teorema pythagoras
AG² = AC² + CG²
AG² = 13² + 9²
AG² = 169 + 81
AG² = 250
AG = √250
AG = √25 x 10
AG = 5√10 cm
Tugas 7.3
1. Diketahui panjang sisi suatu kubus 12 cm. Tentukanlah!
a. Gambarlah Kubus tersebut
b. Luas permukaan Kubus
c. Volume Kubus
d. Panjang diagonal bidang
e. Panjang diagonal ruang
f. Luas bidang diagonal
2. Perhatikan bangun berikut!
a. Luas permukaan Balok
b. Volume Balok
c. Panjang AC
d. Panjang CF
Petunjuk Pengisian
1. Kerjakan dalam buku tugas Matematika
2. Cantumkan nomor tugas dan Tanggal Pengerjaan
3. Cantumkan Nama lengkap dan Kelas
4. Kerjakan sesuai dengan instruksi soal.
5. Foto tugas yang telah kalian buat dengan jelas dan tidak blur.
6. Kemudian upload fotonya dengan cara >> KLIK DISINI<<









No comments:
Post a Comment